- Home
- Quantitative
- English
- Reasoning
- IT Officer
- Programming
-
Computer
- Computer Awareness Questions Answers - Set 1
- Computer Awareness Questions Answers - Set 2
- Important Abbreviations Computer Awareness Questions Answers
- Important File Extensions Questions Answers
- Computer System Architecture Questions Answers
- MS Office Questions Answers
- MS Excel Questions Answers
- MS PowerPoint Questions Answers
-
GK
- Geography Questions Answers
- Indian History Questions Answers
- World History Questions Answers
- Indian Economy Questions Answers
- Indian Polity and Constitution
- Physics Questions Answers
- Chemistry Questions Answers
- Biology Questions Answers
- First In India
- First In World
- Longest and Largest
- Books and Authors
- Important Days of year
- Countries and Capitals
- Inventions and Inventors
-
Current Affairs
- Current Affairs
- Current Affairs 2018
- Current Affairs 2018 - 2019 PDF
- Current Affairs August 2019
- Current Affairs July 2019
- Current Affairs June 2019
- Current Affairs May 2019
- Current Affairs April 2019
- Current Affairs March 2019
- Current Affairs February 2019
- Current Affairs January 2019
- Current Affairs December 2018
- Current Affairs November 2018
- Current Affairs October 2018
- Current Affairs September 2018
- Govt Jobs
- Exams
- Online Quiz
- You are here
- Home
- Quantitative Aptitude
- Arithmetic Aptitude Questions Answers
- Height and Distance Questions Answers
- Aptitude Question
- Current Affairs 2019
- Current Affairs 2018
- Current Affairs December 2018
- Current Affairs November 2018
- Current Affairs October 2018
- Current Affairs September 2018
- Current Affairs August 2018
- Current Affairs July 2018
- Current Affairs June 2018
- Current Affairs May 2018
- Current Affairs April 2018
- Current Affairs March 2018
- Current Affairs February 2018
- Current Affairs January 2018
- Current Affairs 2018
- Current Affairs PDF
- Current Affairs PDF Download
- Current Affairs July 2019 PDF
- Current Affairs June 2019 PDF
- Current Affairs May 2019 PDF
- Current Affairs April 2019 PDF
- Current Affairs March 2019 PDF
- Current Affairs February 2019 PDF
- Current Affairs January 2019 PDF
- Current Affairs December 2018 PDF
- Current Affairs November 2018 PDF
- Current Affairs October 2018 PDF
- Current Affairs September 2018 PDF
- Current Affairs August 2018 PDF
- Current Affairs July 2018 PDF
- Current Affairs June 2018 PDF
- Current Affairs May 2018 PDF
- Current Affairs April 2018 PDF
- Current Affairs March 2018 PDF
- Current Affairs February 2018 PDF
- Current Affairs January 2018 PDF
Question Detail
A man is watching form the top of the tower a boat speeding away from the tower. The boat makes the angle of depression of 45 degree with the man's eye when at a distance of 60 metres from the tower. After 5 seconds the angle of depression becomes 30 degree. What is the approximate speed of the boat, assuming that it is running in still water ?
- 22 Km/Hr
- 28 Km/Hr
- 32 Km/Hr
- 36 Km/Hr
Answer: Option C
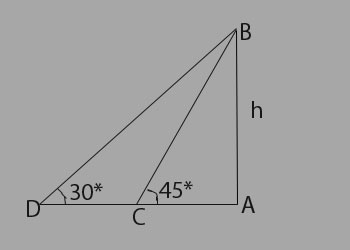
Explanation:
Let AB be the tower and C and D be the positions of the boat.
\begin{aligned}
then \angle{ACB}=45^{\circ}, \angle{ADB}=30^{\circ}, \\
AC = 60&m \\
Let& AB = h \\
=>\frac{AB}{AC} = tan&45^{\circ} = 1 \\
=> AB = AC = 60&m \\
and, \frac{AB}{AD} = tan&30^{\circ} = \frac{1}{\sqrt{3}} \\
=> AD = AB*\sqrt{3} = 60\sqrt{3}&m \\
=> CD = AD-AC = 60\sqrt{3}-60\\
=> CD = 60(\sqrt{3}-1) m \\
\text{We Know Speed = }\frac{Distance}{Time} \\
=> Speed = \left[\frac{60(\sqrt{3}-1)}{5} \right]m/sec
= 12*0.73&m/sec \\
\text{Please note answer we need in Km/Hr} \\
=> Speed = 12*0.73*\frac{18}{5} Km/Hr \\
=> Speed = 31.5 & Km/hr, \\
\text{Which is approx 32 Km/Hr}
\end{aligned}
1. The Top of a 15 metre high tower makes an angle of elevation of 60 degree with the bottom of an electric pole and angle of elevation of 30 degree with the top of pole. Find the height of the electric pole.
- 7 metre
- 8 metre
- 9 metre
- 10 metre
Answer: Option D
Explanation:
Let AB be the tower and CD be the electric pole.
\begin{aligned}
\angle{ACB}=60^{\circ}, \angle{EDB}=30^{\circ}, \\
AB = 15&m \\
Let & CD = h, \text{ then}, \\
BE = AB-AE = AB - AE = 15-h\\
\frac{AB}{AC} = tan 60^{\circ} = \sqrt{3} \\
=> AC = \frac{AB}{\sqrt{3}} \\
=> AC = \frac{15}{\sqrt{3}} \\
and, & \frac{BE}{DE} = tan 30^{\circ} = \frac{1}{\sqrt{3}} \\
=> DE = (BE*\sqrt{3}) \\
= \sqrt{3}(15-h) \\
Now, & AC = DE \\
=> \frac{15}{\sqrt{3}} = \sqrt{3}(15-h) \\
=> 3h = 45-15 \\
=> h = \frac{30}{3} = 10 m
\end{aligned}
2. A man standing at a point C is watching the top of a tower, which makes an angle of elevation of 30 degree. The man walks some distance towards the tower to watch its top and the angle of elevation become 60 degree. What is the distance between the base of the tower and point C.
- \begin{aligned} 4\sqrt{3} meter \end{aligned}
- \begin{aligned} 2\sqrt{3} meter \end{aligned}
- \begin{aligned} \sqrt{3} meter \end{aligned}
- Data is inadequate
Answer: Option D
Explanation:
Please refer to the image. One of the AB, AD and CD must be given. So data is inadequate.
3. A toy leaves the earth at a point A and rises vertically at uniform speed. After two minutes of vertical rise boy finds the angular elevation of the balloon as 60°.
If the point at which boy is standing is 150 m away from point A, what is the speed of the toy ?
- .98 meter/second
- 1.08 meter/second
- 1.16 meter/second
- 2.08 meter/second
- 2.16 meter/second
Answer: Option E
Explanation:
Let boy is standing at C position and A is that position from where toy left eartg and B is the position of the toy after 2 minutes.
\begin{aligned}
\text{ Given that CA = 150 m } \\
\text{Angle is }\angle{ 60 ^{\circ} } \\
tan 60 ^{\circ} = \frac{BA}{CA} \\
BA = 150 \sqrt{3}
\end{aligned}
So distance travelled by toy is,
\begin{aligned}
150 \sqrt{3} \\
\text { Total time taken is = 2 min} \\
= \text {2 * 60 = 120 seconds } \\
Speed = \frac{Distance}{Time} \\
= \frac{150\sqrt{3}}{120} = 1.25\sqrt{3}\\
= \text {1.25 * 1.73 = 2.16 mtr/sec}
\end{aligned}
4. The angle of elevation of the sun, when the length of the shadow of a tree is \begin{aligned}\sqrt{3}\end{aligned} times the height of tree, is :
- 30 degree
- 45 degree
- 60 degree
- 9 degree
Answer: Option A
Explanation:
Let AB be the tree and AC be its shadow, So as per question, shadow of a tree is \begin{aligned}\sqrt{3}\end{aligned} times the height of tree. Let h be the height of the tree, then
\begin{aligned}
\frac{AB}{AC} = tan\theta \\
=> \frac{h}{\sqrt{3}h} = tan\theta \\
=> tan\theta = \frac{1}{\sqrt{3}} \\
=> \theta = 30^{\circ}
\end{aligned}
5. A man is watching form the top of the tower a boat speeding away from the tower. The boat makes the angle of depression of 45 degree with the man's eye when at a distance of 60 metres from the tower. After 5 seconds the angle of depression becomes 30 degree. What is the approximate speed of the boat, assuming that it is running in still water ?
- 22 Km/Hr
- 28 Km/Hr
- 32 Km/Hr
- 36 Km/Hr
Answer: Option C
Explanation:
Let AB be the tower and C and D be the positions of the boat.
\begin{aligned}
then \angle{ACB}=45^{\circ}, \angle{ADB}=30^{\circ}, \\
AC = 60&m \\
Let& AB = h \\
=>\frac{AB}{AC} = tan&45^{\circ} = 1 \\
=> AB = AC = 60&m \\
and, \frac{AB}{AD} = tan&30^{\circ} = \frac{1}{\sqrt{3}} \\
=> AD = AB*\sqrt{3} = 60\sqrt{3}&m \\
=> CD = AD-AC = 60\sqrt{3}-60\\
=> CD = 60(\sqrt{3}-1) m \\
\text{We Know Speed = }\frac{Distance}{Time} \\
=> Speed = \left[\frac{60(\sqrt{3}-1)}{5} \right]m/sec
= 12*0.73&m/sec \\
\text{Please note answer we need in Km/Hr} \\
=> Speed = 12*0.73*\frac{18}{5} Km/Hr \\
=> Speed = 31.5 & Km/hr, \\
\text{Which is approx 32 Km/Hr}
\end{aligned}
Thanks ! Your comment will be approved shortly !
- Copyright 2014 - All rights reserved
- Terms Of Use & Privacy Policy
- Contact Us
- Copyright














