Question Detail
A child is looking for his father. He went 90 meters in the east before turning to his right. He went 20 meters before turning to is right again to look for his father at his uncle's place 30 meters from this point. His father was not there. From there, he went 100 meters to his north before meeting his father in a street. How far did the son meet his father from starting point ?
- 80 metre
- 90 metre
- 100 metre
- 110 metre
Answer: Option C
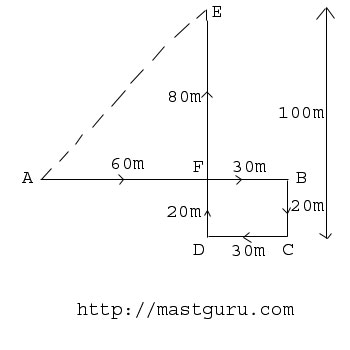
Explanation:
Clearly, the child moves from A to B 90 metres eastwards upto B, then turns right and moves 20 metre upto C, then turns right and moves upto 30 metre upto D. Finally he turns right and moves upto 100 metre upto E.
So AB = 90 metre, BF = CD = 30 metre,
So, AF = AB - BF = 60 metre
Also DE = 100 metre, DF = BC = 20 metre
So, EF = DE - DF = 80 metre
as we can see in image that triangle AFE is a right angled triangle and we are having two sides, need to calculate third one, so we can apply Pythagoras theorem here
\begin{aligned}
A = AE = \sqrt{AF^2 + EF^2} \\
= \sqrt{(60)^2+(80)^2} \\
= \sqrt{3600+6400} \\
= \sqrt{10000} = 100
\end{aligned}
So from starting point his father was 100 metre away.
Videos @mastguru
To Appreciate Our Effort, Please Like Us
